Um dos temas vistos durante o ensino médio é o de matrizes. Muitos estudantes se apavoram ao entrar em contato com esse assunto, pois, a princípio, esse tema realmente parece complicado. Mas, como mostraremos aqui, matriz pode ser um assunto bastante simples, desde que seja bem compreendido.
Então, venha com a gente, pois iremos detalhar tudo o que você precisa saber sobre esse conteúdo!
Sem dúvida nenhuma, a matemática representa uma das matérias mais importantes para o nosso dia a dia. Conhecida também como ciência do raciocínio lógico, essa área do conhecimento se preocupa em estudar os números, além interpretar medidas, quantidades e espaços.
A matemática é ensinada tanto no ensino fundamental quanto no ensino médio, dada a extensão de assuntos que a área engloba. No ensino fundamental, costumamos ver temas mais simples, como aritmética e álgebra. Já no ensino médio, os temas costumam se tornar mais complexos, uma vez que os alunos precisam se capacitar para ingressar no ensino superior.
O que é Matriz?
Matrizes nada mais são do que sistemas voltados para a organização de informações, de modo que os problemas matemáticos sejam resolvidos mais facilmente.
Uma matriz é formada por linhas (filas horizontais) e colunas (filas verticais), as quais são compostas por elementos representados por letras minúsculas. As linhas e colunas vão determinar a ordem de cada matriz. Um conjunto com três linhas e duas colunas, por exemplo, é uma matriz de ordem três por dois.
O conjunto que forma a matriz também é representada por uma letra, mas maiúscula. Essa letra é acompanhada por um índice de dois números (o primeiro número indica a quantidade de linhas, enquanto o segundo, a quantidade de colunas).
O conjunto a seguir, por exemplo, é uma matriz A3x3. Isso indica que o sistema é formado por três linhas, três colunas e nove elementos.
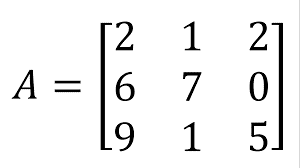
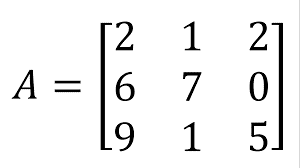
Vale lembrar que, para representar um elemento, basta observar em que posição ele se encontra na matriz. O número 7, por exemplo, deve ser representado pelo elemento a22, pois se encontra na segunda linha da segunda coluna.
Tipos de Matriz
Nós temos quatro tipos principais de matrizes que todo estudante deve conhecer. Abaixo, iremos detalhar cada uma delas.
Matriz Quadrada:
Uma matriz quadrada é aquela em que a quantidade de linhas e a quantidade colunas são iguais. Essas matrizes são representadas por “An”, ou seja, matrizes de ordem n.
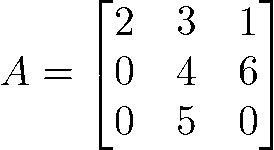
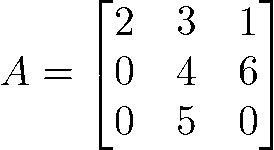
Ainda sobre esse tipo de matriz, é importante ressaltar que existem dois elementos indispensáveis, que são a diagonal principal e a diagonal secundária. A primeira é composta por elementos cujos índices são iguais, enquanto na segunda, os elementos são formados por n + 1 (n = ordem da matriz). Veja o exemplo abaixo.
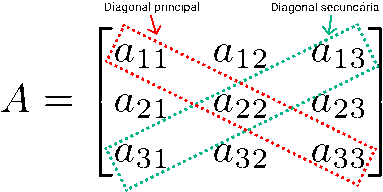
Todos os elementos da diagonal principal possuem um índice formado por números iguais (por exemplo: em a11, 1 é igual a 1). Já na diagonal secundária, todos os índices, quando somados, dão 4 (ordem da matriz + 1 = 3 + 1).
Matriz Identidade:
Uma matriz identidade nada mais é do que uma matriz quadrada, onde os elementos da diagonal principal são iguais ao número um, enquanto os outros elementos são iguais a zero.
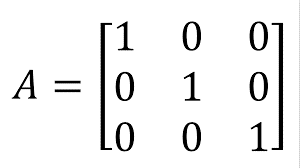
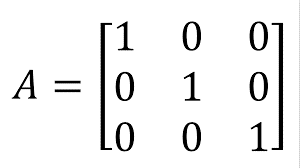
Matriz Nula:
Matrizes nulas são aquelas em que todos os elementos são iguais a zero.
Matriz Oposta:
Matrizes opostas são matrizes de mesma ordem, cujos elementos correspondentes são opostos (aij = -bij).
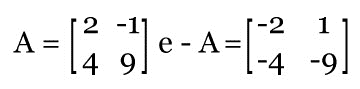
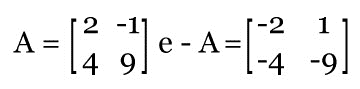
Matriz Como Resolver
Os cálculos com matrizes podem envolver três das quatro operações fundamentais: adição, subtração e multiplicação. Explicaremos cada uma a seguir.
Adição:
Ao realizar a adição de duas matrizes, o resultado será uma terceira matriz. Por exemplo: a soma da matriz A com a matriz B resultará na matriz C.
Cada elemento da nova matriz será formado pela adição de um elemento da matriz A e outro elemento da matriz B. Portanto, para essa equação, é necessário que as matrizes possuam a mesma ordem.
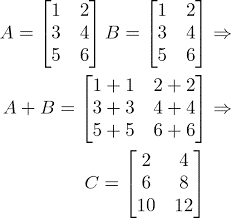
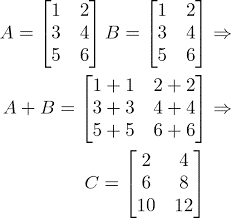
Subtração:
A subtração de matrizes segue o mesmo princípio da adição. As matrizes precisam ser de mesma ordem, e os elementos, em vez de somados, devem ser subtraídos.
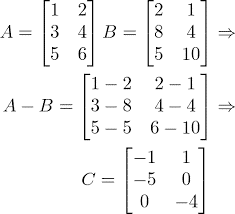
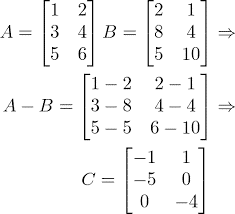
Multiplicação:
Na multiplicação de matrizes, para que a conta seja possível, a quantidade de colunas da matriz A deve ser igual a quantidade de linhas da matriz B. O produto dos elementos dessas duas matrizes irá originar a matriz C.
Cada elemento da coluna deverá ser multiplicado por cada elemento das linhas, como é explicitado no exemplo:
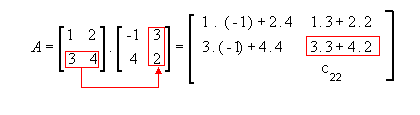
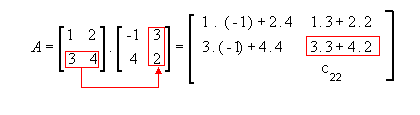
Exercícios de Matriz
Para que fique mais claro esse assunto, iremos detalhar, a seguir, a resolução de dois exercícios que envolvem matrizes.
Primeiro exemplo:
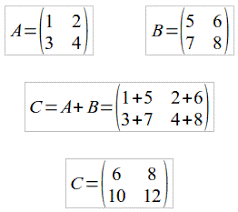
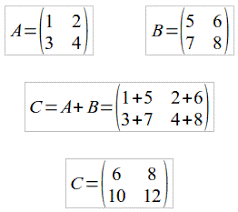
Na questão acima, temos a soma de duas matrizes, A + B. Ambas possuem a mesma ordem (dois por dois) e resultarão, portanto, numa matriz de ordem igual.
Para obter a matriz C, cada elemento da matriz A (a11, a12, a21, a22) deverá ser somado ao elemento correspondente da matriz B (b11, b12, b22, b22). Depois de efetuados todos os cálculos, teremos apenas a matriz C.
Segundo exemplo:
Na questão acima, temos a multiplicação de duas matrizes. Para descobrir os elementos da matriz C, basta multiplicar todos os elementos das linhas da primeira matriz pelos elementos das colunas da segunda matriz. Veja como:
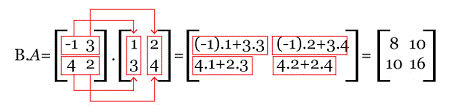
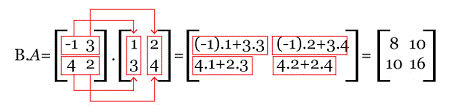
- (b11 x a11) + (b12 x a21) = c11 = 8
- (b11 x a12) + (b12 x a22) = c12 = 10
- (b12 x a11) + (b12 x a21) = c21 = 10
- (b12 x a12) + (b12 x a22) = c22 = 16
