Artigos populares
Desenhos para Colorir Lol
Cada vez mais queridas entre as crianças, as bonecas Lol podem ser encontradas como atividade na internet para que as crianças possam imprimir, colorir...
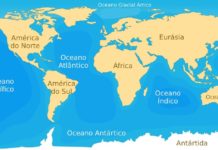
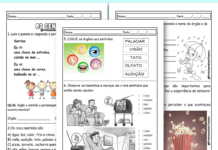
Atividades de Português para 3º Ano
As crianças que estão no terceiro ano do ensino fundamental já iniciam desde o primeiro ano o seu aprendizado com as letras, palavras, textos...
Molde de Coroa em EVA
Antigamente, a coroa era a simbologia mais importante da realeza. Por ser colocada acima da cabeça, a coroa representava elevação, poder e superioridade. Hoje,...
Atividades com Vogais
O Alfabeto possui 26 letras no total e dentre elas são 5 vogais, A, E, I, O, U. Todas as palavras da Língua Portuguesa...
Moldes de Letras para Imprimir
Para quem está aprendendo a escrita, principalmente as crianças, uma ótima alternativa para o aprendizado é o Moldes de Letras para imprimir, juntamente com...